
TECHNICAL NOTE
Quloud-Mag解説(3)シミュレーション適用紹介
INTRODUCTION
EXAMPLE 1
Quloud-Magを用いた磁性材料シミュレーションの例1:ネオジム磁石
まずは代表的な強磁石のネオジム磁石に適用した結果をご紹介する。ネオジム磁石は現在最もよく用いられている磁石であり、現在最強の磁石として知られている材料です。ところが、このネオジム磁石は低温領域(その閾値はスピン再配向温度と呼ばれており、実験的に100K程度であることが知られている)で“スピン再配向”と呼ばれる磁石の性質を弱める振る舞いが知られていました。また、このスピン再配向を引き起こす物理としては結晶場効果によるものと言われており、この物理を再現するためには磁気異方性に結晶場効果を繰り込んで、実験値に対してフィッティングするという現象論的アプローチが取られてきました。このままの現象論的アプローチに頼ったままでは真に新物質予言が難しい状況でした。このような背景の下、我々はこのネオジム磁石に対してQuloud-Magを適用した結果が次の通りです。
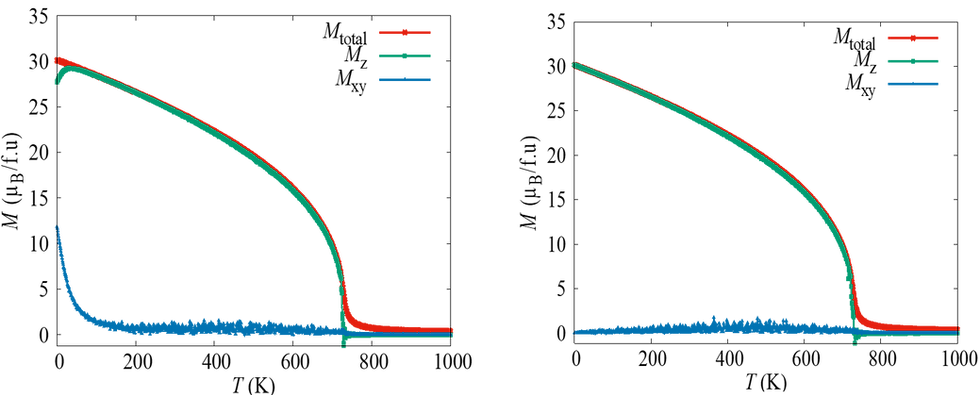
モンテカルロシミュレーションによる、磁気モーメントの温度依存性の結果をご覧いただいています。シミュレーション結果によって、磁気モーメントの絶対値(赤い曲線)は低温に行くに従い単調増加している様子が見えます。一方で、磁気モーメントのz成分(緑色曲線)は100K程度から減少に転じており、変わってxy面内成分が急激に立ち上がっている様子がわかります。つまり、100K程度を境目に磁気モーメントがz軸方向からxy面内軸方向に寝始めていることがわかります。これはまさに実験で見られた“スピン再配向”の再現が実験値なしに再現されたことを意味しています。これは世界初の成果です。我々はこのスピン再配向を引き起こしている原因を明確にするために、モンテカルロシミュレーションのハイゼンベルグハミルトニアンからジャロシンスキー守谷相互作用の項を落としてシミュレーションしました。その結果が右側にグラフになっています。ご覧のように、左のシミュレーション結果とは全く異なる振る舞いをしていることが示されました。つまり、スピン再配向を引き起こしている物理はより原子レベルから見た時には、ジャロシンスキー守谷相互作用であり、これによって実験値なしにスピン再配向温度を予言できるようになったことはシミュレーションの効果です。スピン再配�向現象は、ネオジム磁石だけに限った現象ではありません。他のレアアース磁性体でも見られる現象です。比較として、他の物質での計算結果を紹介します。
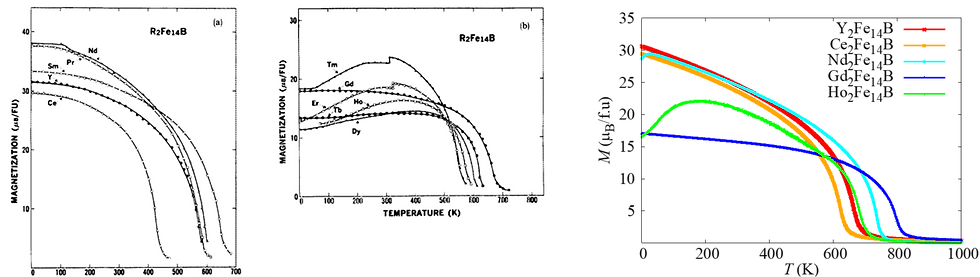
左2つのグラフは論文S. Hirosawa et al, J. Appl. Phys. 59, 873 (1986). から転載した実験の様子です。一方で、右側のグラフは我々のQuloud-Magを用いたシミュレーションの結果です。よく実験を再現している様子がわかります。このように、Quloud-Magは磁石材料の磁気特性を解明・予言する上で極めて強力な道具となります。ここで得られた成果は論文H. Tran and Y. Matsushita, Applied Materials Today 32, 101825(2023) . で報告いたしました。
EXAMPLE 2
Quloud-Magを用いた磁性材料シミュレーションの例2:ナノ粒子系
Quloud-Magをナノ磁性粒子に適用した結果2つをご紹介します。L10型FePtはネオジム磁石をも超える磁気異方性を持った材料として知られており、磁気テープなどのメモリデバイス材料として活用されているものになっております。磁気メモリデバイスには、磁気モーメントの向き(上向きか下向きか)によってデジタルの0・1データが記録さ�れ、十分に長い期間に渡って書き込まれたデータを消失せずに保持し続けることが求められます。あまりにもナノ粒子が小さすぎると十分に長い期間のデータ保持が難しくなり、一方でナノ粒子が大きすぎると単位面積あたりのデータ容量が小さくなってしまいます。十分にデータ保持期間を維持しながら、データ容量を増やすにはナノ粒子系に対する磁性材料の振る舞いを理解することが重要です。このような背景の下、我々はQuloud-Magを用いてL10型FePtのナノ粒子特性をシミュレーションによって求めました。
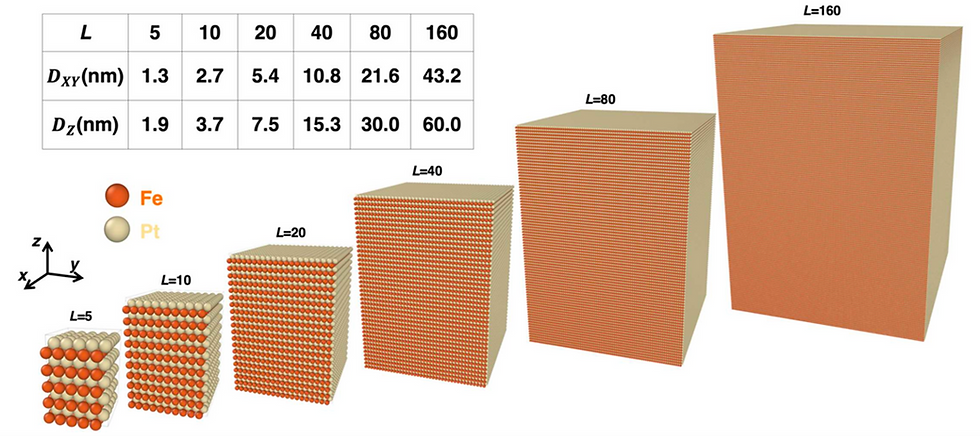
シミュレーションで扱った様々なサイズのL10型FePtのナノ粒子の結晶構造です。

モンテカルロシミュレーションによる計算結果を示しています。左側にグラフにおいて、赤い曲線はバルク(結晶)の時の温度の振る舞いです。シミュレーションによるキュリー温度は600K程度と予測されていることが読み取れます。一方で、ナノ粒子�径を小さくしていくと、キュリー温度が少しずつ低くなっていく様子が見られます。特に、一番小さいナノ粒子径(青い曲線)では明確なキュリー温度を示さないことも読み取れます。これは後に示す超常磁性状態となっていることを示しています。右側のグラフでは、各粒子径に対して、キュリー温度をバルク時の温度で規格化したものを示しています。また、それと同時に、実験で得られた振る舞いも合わせてプロットされています。グラフの通り、粒子径を小さくしていくことによって、キュリー温度が低くなっていくこと、またその振る舞いは実験をもよく再現していることがわかります。
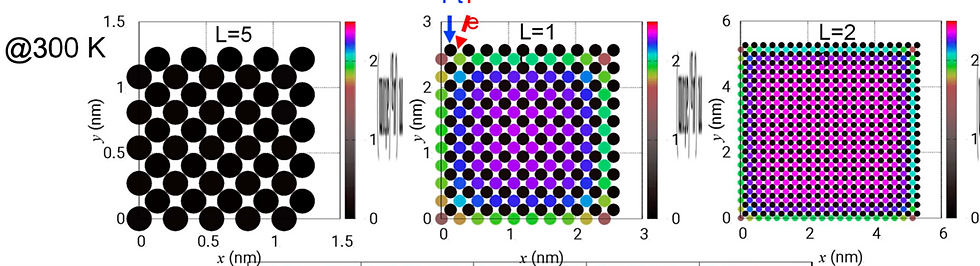
これは300Kにおける各ナノ粒子に対する断面を見た時の(時間平均)磁気モーメントの分布の様子です。一番左の最小径ナノ粒子において、磁気モーメントが消失している様子がうかがえます。これは超常磁性と呼ばれている現象であり、各原子サイトで磁気モーメント自体は存在しながらも、粒子径が小さくなりすぎた為に粒子径全体の磁気異方性エネルギーが温度揺らぎよりも小さくなり、時間平均をとった時の磁気モーメントが実質ゼロとなって見える現象です。一方で、粒子径を大きくしていくとその特にその中心付近において磁気モーメントが生き残ってくる様子が見られます。このように全て実験値なしに超常磁性状態から強磁性ナノ粒子まで統一的にシミュレーションできることが示されました。得られた計算結果は論文H. Tran and Y. Matsushita, Scripta Materialia 242, 115947(2024).にて発表を行いました。

上ではナノ粒子として強磁石に対する振る舞いを見ました。我々は軟磁性体に対するナノ粒子効果に関してもシミュレーションを行なっています。その1つの結果として、γ-Fe2O3の結果もご紹介します。
モンテカルロシミュレーションによる計算結果を示しています。シミュレーションによるキュリー温度は1200K程度と予測されていることが読み取れます。一方で、ナノ粒子径を小さく��していくと、キュリー温度が少しずつ低くなっていく様子がL10型FePtの時と同様に見られます。右側のグラフでは、各粒子径に対して、キュリー温度をバルク時の温度で規格化したものを示しています。
EXAMPLE 4
Quloud-Magを用いた磁性材料シミュレーションの例4:磁気熱量効果
Quloud-Magを用いた磁気熱量効果シミュレーションの結果をご紹介します。近年、冷媒ガスに変わる次世代冷却方法として、磁気熱量効果が注目を�集めています。より大きな磁気熱量効果を示す磁性材料探索が活発化しています。磁気熱量効果の大きさを測る指標としては、エントロピー変化という物理量が挙げられます。エントロピー変化が大きな物質であればあるほど、大きな磁気熱量効果を示す材料であることを示しています。磁気熱量効果は1次の磁気相転移において巨大な値を取ることが知られており、1次の磁気相転移を示す物質の発見は大きな注目を集めます。特に、冷却方法としてこれら材料を用いようとすると、所望する温度に1次磁気相転移が来るように材料設計を行なってやる必要があり、材料研究の舞台となります。どのような元素をどの程度混ぜ込むと1次相転移温度をどれくらい変えることができるのかは、シミュレーションが強みを発揮する格好の対象です。ここでは、1次磁気相転移を示す物質として注目されているLa-Fe-Si系材料に対して、元素ドープを行った時の1次磁気相転移温度の様子を計算しました。

左図がLa-Fe-Si系の結晶構造であり、La原子やFe原子を別の元素XやYに部分的に置換した際の、1次磁気相転移温度(キュリー温度)の変化の様子をプロットしたものです。
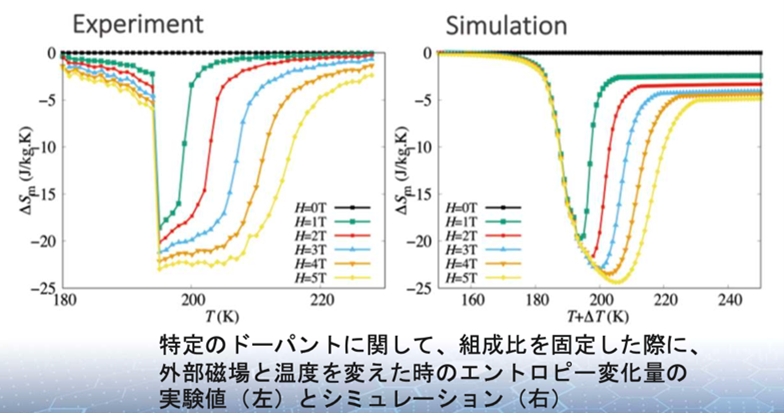
また、La-Fe-Si系のエントロピー変化量をシミュレートした際の実験値(左図)とシミュレーション結果(右図)です。図からわかるように、ピークの高さであったり、温度の幅であったり、よく実験を再現している様子がわかります。このように、シミュレーションでは新規磁気熱量効果を示す材料探索にも効果的であることがわかります。
EXAMPLE 3
Quloud-Magを用いた�磁性材料シミュレーションの例3:磁気損失シミュレーション
Quloud-Magを磁気損失シミュレーション、特に複素透磁率のシミュレーションをご紹介します。複素透磁率は物質の磁気特性を表す基礎物性パラメータの1つであり、その実数部は磁場と磁束密度の比率を表し、虚数部はある振動数を持つ振動磁場に対するエネルギー吸収量を表す量です。特に、5Gや6G用の磁性材料としては、複素透磁率の虚部の小さい物質が探索され、省エネデバイスとして重要な要素になっています。Quloud-Magでは複素透磁率に関して実験値なしに予言を行うことができる世界唯一のソフトウェアとなっています。
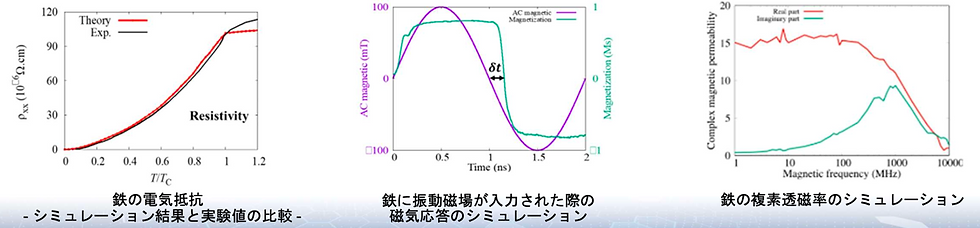
左図には、モンテカルロシミュレーションの結果を示しており、鉄の電気抵抗のシミュレーション結果(赤い曲線)と実験値(黒い曲線)との比較を示しています。横軸は温度であり、キュリー温度で規格化され、縦軸には電気抵抗を示しています。鉄のキュリー温度はおおよそ1000Kであり、図から0Kから1000Kに渡るまで広範囲に実験とシミュレーション結果はよく再現されています。鉄のような磁性体の電気抵抗を再現するには、フォノンによる散乱だけではなく、磁気の散乱効果も取り込まなくてはならず、この結果からも、非常に高い精度で有限温度での磁気特性が再現できていることが読み取れます。エネルギー損失を計算する際には、渦電流によるエネルギー損失が1つの要素になっていますが、渦電流由来のエネルギー損失を計算する際に重要になるのが電気抵抗です。次に、中央の図と右側の図は、マイクロマグネティックシミュレーションによる結果を示しています。中央の図においては、外部磁場(紫色の曲線)に対して鉄の磁気モーメントの応答(緑色の曲線)が示されています。まず、外部磁場がない初期状態においては、磁気モーメントがゼロになっているが、これは鉄内に磁区が複数存在し、マクロに見るとそれが互いに打ち消しあって磁気モーメントがゼロである状態を意味します。実際の鉄も、外部磁場がない状況だと磁石としての性質は影を潜めています。そのような状況を再現しています。その状況で、外部磁場を導入していくと、外部磁場に応答し、互いに磁気モーメントが有限な値を持つようになります。一方、外部の振動磁場が1[ns]後からは逆向きを向き始めますが、鉄はすぐにはその外部磁場には応答できずに応答の遅れδtが生じてきます。応答の遅れを伴いながら、磁気モーメントは外部磁場に追随し、逆向きにフリップする様子も見られます。実は、この応答の遅れδtがエネルギー損失を表す重要な量になっています。遅れが大きければ大きいほど、エネルギー損失は増大します。実際に、このδtに対して変換式を用いると、右図に示す複素透磁率を計算することができます。複素透磁率の実数部(赤い曲線)と虚数部(緑色曲線)です。横軸振動数に対して、縦軸の透磁率がプロットされています。見ていただくように、1GHzにおいて、虚数部がピーク構造を持ち、エネルギーを最大限に吸収していることがわかります。実際に、実験的にも純鉄において1GHzにおいて、虚数部がピーク構造を持つことが知られており、このシミュレーション結果はよく実験を再現していることがわかります。
EXAMPLE 5
Quloud-Magを用いた磁性材料シミュレーションの例5:スキルミオン材料の探索
Quloud-Magを用いた新規磁性材料探索の例をご紹介します。ここではスキルミオン材料の探索を行った例を紹介します。近年、次世代高密度メモリや、量子コンピュータデバイス材料としてスキルミオンという磁性材料が注目を集めています。スキルミオンは、スピンが渦を巻いたスピン構造を持っており、渦の巻き方が時計回りと反時計回りの2種類が存在します。スキルミオンがあるなしを0・1のデジタル情報に対応付けたり、スキルミオンの時計回り・反時計回りを0・1のデジタル情報に対応付けたりさせることにより、次世代のコンピュータを構築しようというものです。特に、メモリとして使う場合には、渦の大きさが記録容量に直結することからできる限り小さなスキルミオンというのが好ましいです。さらには、時計回り・反時計回りを制御可能な材料というものが必要となってきます。これまでスキルミオン材料としては、空間反転対称性が破れた結晶の表面や界面で報告されてきたものが多数です。また、その多くは空間反転対称性の破れた時に出現するジャロシンスキー守谷相互作用に由来して発現したものです。このような背景の下、我々は2次元層状物質であるMCl3(M:遷移金属)のシミュレーションを実施した。ここで、1つ重要なこととして、MCl3は空間反転対称性を有しており、一見するとジャロシンスキー守谷相互作用が発現しない状況に見えることです。しかし、局所的に見ると空間反転対称性を破っており、実はジャロシンスキー守谷相互作用が非ゼロとなりうることがシミュレーションからわかりました。2次元物質中でジャロシンスキー守谷相互作用が有限となることから、スキルミオンが発現しうることがわかりました。
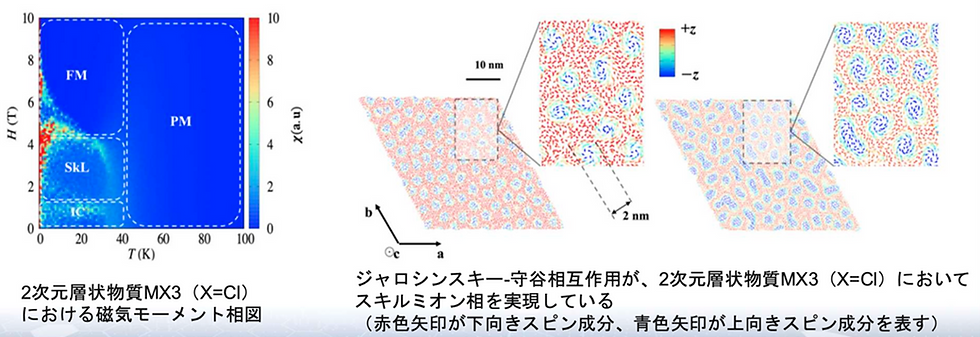
左図には、モンテカルロシミュレーションによって得られた結果を示し、外部磁場と温度による相図を示しています。温度が十分に高い領域においては、常磁性相が出現していることがわかります。温度が低い、外部磁場が大きい領域には強磁性相が出現していることがわかります。一方で、温度が低く、外部磁場が中程度の領域においてスキルミオン相が出現していることが今回シミュレーションで初めてわかりました。これはまだ実験的には確認されていませんが、2次元物質で初めての報告例です。単層でも積層構造でも現れるスキルミオン相であることがわかりました。右図には、モンテカルロシミュレーションで得られたある瞬間のスピン構造のスナップショットとなっています。シミュレーション結果わかったこととして、今回見出されたスキルミオン半径は直径2nmであり、これは過去見出されたスキルミオンと比べても世界最小径です。さらに、遷移金属を変えることにより、スキルミオンの時計回り・反時計回りが変わっていることを示し、このことはゲート電界でスキルミオンの渦の巻き方を制御できる可能性を示しています。このように、Quloud-Magを用いると新規磁性材料探索にも有効なものであることがわかりました。得られたシミュレーション結果は論文H. Tran and Y. Matsushita, Scripta Materialia 239, 115799(2024).にまとめて報告しました。

